Makalah LOGIKA MATEMATIKA

KATA PENGANTAR

Assalamualaikum Warohmatullahi Wabarokatuh

Puji syukur kita panjatkan kepada Allah Subkhanallahuwata’ala. Sholawat serta salam kita kirimkan kepada junjungan Nabi besar Muhammad Sholallahu’alaihi Wassalam, karena atas hidayah-Nyalah paper ini dapat diselesaikan. Paper ini penulis sampaikan kepada pembina Mata Kuliah Pembelajaran Matematika SMA bapak Ariyanto, sebagai tugas pendalaman pembelajaran Matematika.

Tidak lupa penulis ucapkan terima kasih kepada bapak/ibu dosen Matematika yang telah mencurahkan ilmunya kepada penulis, sehingga penulis dapat menyelesaikan dengan lancar dalam menulis paper ini.

Selanjutnya kami mohon kepada bapak dosen khususnya dan pembaca pada umumnya, bila ada kesalahan atau kekurangan dalam paper ini, baik dari segi bahasa maupun kontennya, penulis mengharapkan kritik dan saran yang bersifat membangun kepada semua pembaca demi lebih baiknya karya-karya tulis yang akan datang.

Wassalamu’alaikum Warohmatullahi Wabarokatuh.

Surakarta, 30 Maret 2016

Penulis

DAFTAR ISI

KATA PENGANTAR ……………………………................................................ii

DAFTAR ISI……………………………...............................................................iii

BAB I : PENDAHULUAN

A. Latar Belakang Masalah …………………………...…...................................1

B. Rumusan Masalah ……………………………........... ....................................1

C. Tujuan ……………………………...........................................……………...2

BAB II : PEMBAHASAN

A. Pengertian Logika Matematika ……………………………............................3

B. Pernyataan ……………………………............................................................3

C. Kata Hubung Kalimat…………………………….......................................... 4

D. Negasi dari Pernyataan Majemuk…………………………………………..…9

E. Kontradiksi, Tautologi, dan Ekuivalensi Pernyataan-Pernyataan

Majemuk……………………………………………………………………..12

F. Hukum-Hukum Logika ……………………………...................................13

G. Pernyataan Berkuantor............................................................................14

H. Ingkaran Pernyataan Berkuantor..............................................................15

I. Validitas Pembuktian..............................................................................16

J. Bukti dalam Matematika................................................................................18

K. Latihan Soal……………………………........................................................20

L. Kunci Jawaban……………………………....................................................21

BAB III : PENUTUP

A. Kesimpulan.....................................................................................................23

B. Saran ..............................................................................................................23

DAFTAR PUSTAKA ................................................................................................24

BAB 1

PENDAHULUAN

A. Latar Belakang Masalah

Suatu kenyataan yang tidak dapat dibantah bahwa logika, penalaran dan argumentasi sangat sering digunakan dalam kehidupan nyata sehari-hari, didalam mata pelajaran matematika maupun mata pelajaran lainnya. Dalam arti luas, logika adalah suatu cabang ilmu yang mengkaji penurunan-penurunan kesimpulan yang shahih dan yang tidak shahih. Karenanya logika sangat berguna bagi siswa, disamping dapat meningkatkan daya nalar atau proses berfikir yang terjadi di saat menurunkan dan menarik kesimpulan dari pernyataan yang diketahui benar atau dianggap benar, namun dapat diaplikasikan di dalam kehidupan nyata mereka sehari-hari. Tujuan pembelajaran logika matematika pada dasarnya adalah agar para siswa dapat menggunakan aturan-aturan dasar logika matematika untuk penarikan kesimpulan.

Oleh karena itu, kompetensi yang hendak dicapai adalah agar para siswa memiliki kemampuan dan keterampilan dalam hal mengembangkan dan memanfaatkan logika yang dimiliki serta menambah pengetahuan tentang mata pelajaran ini.

B. Rumusan Masalah

1. Apa pengertian dari logika matematika ?

2. Apa saja kata hubung kalimat pernyataan majemuk ?

3. Bagaimana ingkaran dari pernyataan majemuk ?

4. Apa saja hukum-hukum logika ?

5. Apa saja yang digunakan untuk penarikan kesimpulan ?

C. Tujuan

1. Untuk mengetahui pengertian dari logika matematika.

2. Untuk mengetahui kata hubung kalimat penyataan majemuk.

3. Untuk mengetahui ingkaran dari pernyataan majemuk.

4. Untuk mengetahui hukum-hukum logika.

5. Untuk mengetahui penarikan kesimpulan.

BAB 2

PEMBAHASAN

A. Pengertian Logika Matematika

Logika Matematika atau Logika Simbol ialah logika yang menggunakan bahasa Matematika, yaitu dengan menggunakan lambang-lambang atau simbol- simbol.

Keuntungan atau kekuatan bahasa simbol adalah: ringkas, univalent/bermakna tunggal, dan universal/dapat dipakai dimana-mana.

B. Pernyataan

Kalimat adalah rangkaian kata yang disusun menurut aturan bahasa yang mengandung arti. Pernyataan adalah kalimat yang mempunyai nilai benar atau salah, tetapi tidak sekaligus benar dan salah (pernyataan disebut juga preposisi, kalimat deklaratif). Benar diartikan ada kesesuaian antara apa yang dinyatakan dengan keadaan yang sebenarnya. Perhatikan beberapa contoh berikut!

1. Al-Quran adalah sumber hukum pertama umat Islam

2. 4 + 3 = 8

3. Rapikan tempat tidurmu!

Contoh nomor 1 bernilai benar, sedangkan contoh nomor 2 bernilai salah, dan keduanya adalah pernyataan. Kalimat 3 di atas tidak mempunyai nilai benar atau salah, sehingga bukan pernyataan.

a) Kalimat Terbuka

Adalah kalimat yang belum tentu bernilai benar atau salah. Kalimat terbuka biasanya ditandai dengan adanya variabel (peubah). Jika variabelnya diganti dengan konstanta dalam semesta yang sesuai maka kalimat itu akan menjadi sebuah pernyataan.

Variabel (Peubah) adalah lambang yang menunjukkan anggota yang belum tentu dalam semesta pembicaraan, sedangkan konstanta adalah lambang yang menunjukkan anggota tertentu dalam semesta pembicaraan. Pengganti variabel yang menyebabkan kalimat terbuka menjadi pernyataan yang bernilai benar, disebut selesaian atau penyelesaian.

Contoh kalimat terbuka :

1. yang duduk di bawah pohon itu cantik rupanya

2. x + 2 = 8

b) Pernyataan Majemuk

Logika merupakan sistem matematika artinya memuat unsur-unsur yaitu pernyataan-pernyataan dan operasi-operasi yang didefinisikan. Operasi-operasi yang akan kita temui berupa kata sambung logika :

1) Merupakan lambang operasi untuk negasi

2) Merupakan lambang operasi untuk konjungsi

3) Merupakan lambang operasi untuk disjungsi

4) Merupakan lambang operasi untuk implikasi

5) Merupakan lambang operasi untuk biimplikasi

C. Kata Hubung Kalimat

1. Ingkaran atau Negasi

Ingkaran/Negasi dari suatu pernyataan adalah pernyataan lain yang diperoleh dengan menambahkan kata ”tidak” atau menyisipkan kata ”bukan” pada pernyataan semula. Ingkaran dari suatu pernyataan p disajikan dengan lambang atau –p atau ~p, dan dibaca: ”tidak p”. Bila peryataan p bernilai benar, maka ingkarannya bernilai salah dan sebaliknya.

Contoh Soal :

Misalkan pernyataan

p : Tembakau yang mengandung nikotin.

Ingkaran penyataan p

~ p : Tidak benar bahwa tembakau mengandung nikotin.

Dengan tabel kebenaran

2. Konjungsi

Pernyataan p dengan q dapat digabung dengan kata hubung logika “dan” sehingga membentuk pernyataan majemuk “p dan q” yang disebut konjungsi. Konjungsi “p dan q” dilambangkan dengan “p Ù q”. Konjungsi dua pernyataan p dan q bernilai benar hanya jika kedua pernyataan komponennya bernilai benar. Dan jika salah satu atau kedua pernyataan komponennya salah, maka konjungsi itu salah.

Dengan tabel kebenaran

Contoh Soal :

Jika, p : Ima anak pandai

q : Ima anak cekatan

maka p ∧ q : Ima anak pandai dan cekatan

Pernyataan p ∧ q bernilai benar jika Ima benar-benar anak pandai dan benar-benar anak cekatan.

3. Disjungsi/ Alternasi

Pernyataan p dengan q dapat digabung dengan kata hubung logika “atau” sehingga membentuk pernyataan majemuk “p atau q” yang disebut disjungsi. Disjungsi p atau q dilambangkan dengan “p Ú q”. Dalam kehidupan sehari-hari, kata “atau” dapat berarti salah satu atau kedua-duanya, dapat pula berarti salah satu tetapi tidak kedua-duanya.

Berdasarkan pengertian di atas, dua buah pernyataan yang dihubungkan dengan ”atau” merupakan disjungsi dari kedua pernyataan semula. Dari pengertian kata “atau” di atas maka muncul dua macam disjungsi yaitu sebagai berikut.

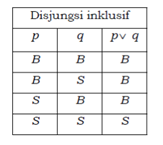
a) Disjungsi inklusif, yaitu dua pernyataan yang bernilai benar apabila paling sedikit satu dari keduanya bernilai benar yang diberi simbol “∨". Untuk disjungsi inklusif dua pernyataan p atau q ditulis p ∨ q. sebagai contoh sekarang perhatikan pernyataan berikut ini, “Andi seorang siswa yang pintar atau seorang atlit berbakat”. Pernyataan itu akan menimbulkan penafsiran “Andi seorang siswa yang pintar, atau seorang atlit yang berbakat, mungkin kedua-duanya”. Pernyataan dengan tafsiran seperti itu merupakan contoh disjungsi inklusif. Untuk contoh yang lain perhatian contoh berikut ini.

1) Persegi memiliki empat sisi atau empat sudut.

2) Adi membawa pensil atau bolpoin.

Tabel kebenaran disjungsi inklusif di berikan sebagai berikut.

b) Disjungsi eksklusif

Disjungsi eksklusif, yaitu dua pernyataan bernilai benar apabila hanya satu dari dua pernyataan bernilai benar yang diberi simbol “⊻”. Disjungsi eksklusif dua pernyataan p dan q ditulis p ⊻ q. Sekarang perhatikan pernyataan sebelumnya lagi, “Andi seorang siswa yang pintar atau seorang atlit berbakat”. Pernyataan itu akan menimbulkan penafsiran “Andi seorang siswa yang pintar, atau seorang atlit yang berbakat, tetapi tidak kedua-duanya (dipilih salah satu)”. Pernyataan dengan tafsiran seperti itu merupakan contoh disjungsi eksklusif. Untuk contoh yang lain perhatikan contoh berikut ini.

1) Adika lahir di Bali atau di Surabaya

2) Dua garis pada satu bidang sejajar atau berpotongan.

Tabel kebenaran disjungsi ekslusif di berikan sebagai berikut.

Catatan : Jika dalam suatu soal tidak diberikan keterangan, maka disjungsi yang dimaksud adalah disjungsi inklusif.

4. Implikasi

Implikasi “jika p maka q” dilambangkan dengan “p Þ q”. Dalam implikasi p ⇒ q, p disebut hipotesa (anteseden) dan q disebut konklusi (konsekuen). Bernilai benar jika anteseden salah atau konsekuen benar, anteseden dan konsekuen sama-sama benar, dan anteseden dan konsekuen salah, dan bernilai salah jika antesedennya bernilai benar, sedangkan konsekuennya salah.

Dengan tabel kebenaran

Contoh soal:

Jika, p : Matahari bersinar

q : udara terasa hangat

Jadi, p Þ q : “Jika matahari bersinar maka udara terasa hangat”,

Jadi, bila kita tahu bahwa matahari bersinar, kita juga tahu bahwa udara terasa hangat. Berdasarkan pernyataan diatas, maka untuk menunjukkan bahwa udara tersebut hangat adalah cukup dengan menunjukkan bahwa matahari bersinar atau matahari bersinar merupakan syarat cukup untuk udara terasa hangat. Sedangkan untuk menunjukkan bahwa matahari bersinar adalah perlu dengan menunjukkan udara menjadi hangat atau udara terasa hangat merupakan syarat perlu bagi matahari bersinar. Karena udara dapat menjadi hangat hanya bila matahari bersinar.

Dari suatu Implikasi p Þ q dapat dibentuk pernyataan majemuk :

Konvers, Invers, dan Kontraposisi

Dari pernyataan berbentuk implikasi dapat kita turunkan pernyataan-pernyataan baru yang disebut invers, konvers, dan kontraposisi.

Ingkaran dari Implikasi Konvers, Invers dan Kontraposisi (Husein: 3013)

a) Ingkaran Konvers: ~ (p Þ q) º (q Ù ~ p)

b) Ingkaran Invers : ~(~ p Þ~ q) º ~p Ù q

c) Ingkaran Kontraposisi: ~(~ q Þ~ p) º ~q Ù p

5. Biimplikasi atau Bikondisional

Biimplikasi “p jika dan hanya jika q” dilambangkan dengan “p Û q”. Biimplikasi bernilai benar apabila anteseden dan konsekuen kedua-duanya bernilai benar atau kedua-duanya bernilai salah. Jika tidak demikian maka biimplikasi bernilai salah.

Dengan tabel kebenaran

Contoh Soal :

p : Saya memakai mantel

q : saya merasa dingin

maka, p Û q = “Saya memakai mantel jika dan hanya jika saya merasa dingin”.

Pengertian kita adalah “Jika saya memakai mantel maka saya merasa dingin” dan juga “Jika saya merasa dingin maka saya memakai mantel”. Terlihat bahwa jika saya memakai mantel merupakan syarat perlu dan cukup bagi saya merasa dingin, dan saya merasa dingin merupakan syarat perlu dan cukup bagi saya memakai mantel. Terlihat bahwa kedua peristiwa itu terjadi serentak.

D. Negasi dari Pernyataan Majemuk

Berikut ini adalah pembahasan tentang negasi pernyataan majemuk, yaitu negasi suatu konjungsi, disjungsi, implikasi, dan biimplikasi

1. Negasi Suatu Konjungsi

Karena suatu konjungsi p ∧ q akan bernilai benar hanya jika kedua komponennya bernilai benar. Maka negasi suatu konjungsi p ∧ q adalah ~p ∨ ~q; sebagaimana ditunjukkan tabel kebenaran berikut:

Contoh Soal :

Jika, p : Ima anak pandai, dan

q : Ima anak cekatan.

maka p ∧ q : Ima anak pandai dan cekatan

Pernyataan p ∧ q bernilai benar jika Ima benar-benar anak pandai dan benar-benar anak cekatan.

Apabila p ∧ q jika di negasikan menjadi ~p ∨ ~q

Maka ~p ∨ ~q : Ima bukan anak pandai atau bukan cekatan

2. Negasi Suatu Disjungsi

Negasi suatu disjungsi p ∨ q adalah ~p ∧ ~q sebagaimana ditunjukkan tabel kebenaran berikut:

Contoh soal :

Jika p : Persegi memiliki empat sisi

q : empat sudut

maka, p ∨ q : Persegi memiliki empat sisi atau empat sudut

Apabila p ∨ q dinegasikan menjadi ~p ∧ ~q

Maka ~p ∧ ~q : Persegi tidak memiliki empat sisi dan empat sudut

3. Negasi Suatu Implikasi

Negasi suatu implikasi p ⇒ q adalah p∧~q seperti ditunjukkan tabel kebenaran berikut ini:

Dengan demikian, p ⇒ q ≡ ~[~ (p ⇒ q)] ≡ ~( p ∧ ~q) ≡ ~p ∨ q

Contoh soal:

Jika, p : Matahari bersinar

q : udara terasa hangat

Jadi, p Þ q : “Jika matahari bersinar maka udara terasa hangat”

Apablia p ⇒ q dinegasikan menjadi p∧~q

Maka, p∧~q : matahari bersinar dan udara tidak terasa hangat

4. Negasi Suatu Biimplikasi

Karena biimplikasi atau bikondisional p ⇔ q ekuivalen dengan

(p ⇒ q) ∧ (q ⇒ p);

sehingga:

~ (p ⇔ q) ≡ ~[(p ⇒ q) ∧ (q ⇒ p)]

≡ ~[(~p ∨ q) ∧ (~q ∨ p)]

≡ ~(~p ∨ q) ∨ ~(~q ∨ p)]

≡ (p ∧ ~q) ∨ (q ∧ ~p)

Contoh Soal :

p : Saya memakai mantel

q : saya merasa dingin

maka, p Û q = “Saya memakai mantel jika dan hanya jika saya merasa dingin”.

Apabila p Û q dinegasikan menjadi (p ⇒ q) ∧ (q ⇒ p)

Maka, (p ⇒ q) ∧ (q ⇒ p) : Jika saya memakai mantel maka maka saya merasa dingin dan jika saya merasa dingin maka saya memakai mantel.

E. Kontradiksi, Tautologi, Ekuivalensi Pernyataan-Pernyataan Majemuk

1. Pengertian Kontradiksi

Kontradiksi adalah sebuah pernyataan majemuk yang selalu salah untuk semua kemungkinan nilai kebenaran dari pernyataan-pernyataan komponennya.

Contoh pernyataan: “Junus masih bujang atau Junus bukan bujang” akan selalu bernilai benar tidak bergantung pada apakah junus benar-benar masih bujang atau bukan bujang.

Jika p : junus masih bujang, dan ~p : junus bukan bujang, maka pernyataan diatas berbentuk p ∨ ~p. (coba periksa nilai kebenarannya dengan menggunakan tabel kebenaran). Setiap pernyataan yang bernilai benar, untuk setiap nilai kebenaran komponen-komponennya, disebut tautologi.

2. Pengertian Tautologi

Tautologi adalah sebuah pernyataan majemuk yang selalu benar untuk semua kemungkinan nilai kebenaran dari pernyataan-pernyataan komponennya.

Contoh pernyataan: “Pratiwi seorang mahasiswa dan bukan mahasiswa”. Pernyataan ini selalu bernilai salah, tidak tergantung pada nilai kebenaran dari “Pratiwi seorang mahasiswa” maupun “Pratiwi bukan mahasiswa”.

Jika r : Pratiwi mahasiswa maka ~ r : Pratiwi bukan mahasiswa maka pernyataan di atas berbentuk r ∧ ~ r (Coba periksa nilai kebenarannya dengan menggunakan tabel kebenaran).

Setiap pernyataan yang selalu bernilai salah, untuk setiap nilai kebenaran dari komponen-komponen disebut kontradiksi. Karena kontradiksi selalu bernilai salah,

maka kontradiksi merupakan ingkaran dari tautologi dan sebaliknya.

3. Ekuivalensi Pernyataan – Pernyataan Majemuk

a) implikasi º kontraposisi : p Þ q º ~ q Þ ~ p

b) konvers º invers : q Þ p º ~ p Þ ~ q

c) ~(p Ù q) º ~ p Ú ~ q : ingkaran dari konjungsi

d) ~(p Ú q) º ~ p Ù ~ q : ingkaran dari disjungsi

e) ~(p Þ q) º p Ù ~ q : ingkaran dari implikasi

f) p Þ q º ~ p Ú q

g) ~(p Û q) º (p Ù ~ q) Ú (q Ù ~ p) : ingkaran dari biimplikasi

F. Hukum-Hukum Logika

1. Sifat-Sifat Aljabar Proposisi

2. Hukum-hukum logika :

G. Pernyataan Berkuantor

Pernyataan berkuantor artinya pernyataan yang mengandung ukuran kuantitas atau jumlah. Pernyataan berkuantor mengandung kata semua, setiap, tiap-tiap, ada, terdapat, beberapa dan sebagainya.

Terdapat dua macam kuantor, yaitu :

1. Kuantor Universal.

Disebut juga kuantor umum, ditandai dengan kata : “semua, setiap, tiap-tiap” atau ditulis ("x). Kuantor universal dilambangkan (x),p(x).

Contoh Soal :

a) Semua siswa memakai seragam.

b) Tiap-tiap kelas selalu menjaga kebersihan.

c) Setiap manusia punya kesalahan.

d) Setiap bilangan asli adalah bilangan cacah.

2. Kuantor Eksistensial.

Disebut juga Kuantor Khusus, ditandai dengan kata : “ Ada, terdapat, beberapa “ atau ditulis ($x). Kuantor eksistensial dilambangkan (x), p(x)

Contoh Soal:

a) Ada siswa yang tidak mengerjakan PR.

b) Terdapat bilangan prima yang genap.

c) Beberapa kelas sedang tidak belajar.

H. Ingkaran Pernyataan Berkuantor

1. Ingkaran Kuantor Universal

Ingkaran dari pernyataan majemuk “untuk semua x, sehingga berlaku p(x)” adalah “ada x, sehingga berlaku bukan p(x)”,ditulis ~[("x), p(x)] º ($x), ~p(x)

Contoh Soal :

p : Semua kucing berwarna putih.

-p : Tidak benar bahwa semua kucing berwarna putih.

-p : Ada kucing yang tidak berwarna putih.

Secara umum ingkaran dari semua adalah ada/beberapa, dan dilambangkan :

– ( (x),p(x)) (x), -p(x)

2. Ingkaran Kuantor Eksistensial.

Ingkaran dari pernyataan “ada x, sehingga berlaku p(x)” adalah “untuk semua x, sehingga berlaku bukan p(x)”, ditulis ~[($x), p(x)] º ("x), ~p(x)

Contoh Soal:

p : Adaperempuan yang menjadi presiden.

-p : Tidak ada perempuan yang menjadi presiden.

-p : Semua perempuan tidak menjadi presiden.

Secara umum ingkaran dari Ada/beberapa adalah semua, dan dilambangkan :

– ((x), p(x) ) (x),-p(x)

I. Validitas Pembuktian

1. Premis dan Argumen

Premis adalah pernyataan-pernyataan yang digunakan untuk menarik suatu kesimpulan, sehingga suatu premis dapat berupa aksioma, hipotesa, definisi atau pernyataan yang sudah dibuktikan sebelumnya.

Sedang yang dimaksud dengan argumen adalah kumpulan kalimat yang terdiri atas satu atau lebih premis yang mengandung bukti-bukti (evidence) dan suatu (satu) konklusi. Konklusi ini selayaknya (supposed to) diturunkan dari premis-premis.

2. Validitas Pembuktian (I)

a) Modus Ponen

Premis 1 : p Þ q

Premis 2 : p

Konklusi : q

Contoh Soal :

Premis 1 : Jika saya belajar, maka saya lulus ujian (benar)

Premis 2 : Saya belajar (benar)

Konklusi : Saya lulus ujian (benar)

Baris pertama dari tabel kebenaran kondisional (implikasi) menunjukkan validitas dari bentuk argumen modus ponen.

b) Modus Tolen :

Premis 1 : p Þ q

Premis 2 : ~ q

Konklusi : ~ p

Contoh Soal :

Premis 1 : Jika hari hujan maka saya memakai jas hujan (benar)

Premis 2 : Saya tidak memakai jas hujan (benar)

Konklusi : Hari tidak hujan (benar)

Perhatikan bahwa jika p terjadi maka q terjadi, sehingga jika q tidak terjadi maka p tidak terjadi.

c) Silogisma :

Premis 1 : p Þ q

Premis 2 : q Þ r

Konklusi : p Þ r

Contoh :

Premis 1 : Jika kamu benar, saya bersalah (B)

Premis 2 : Jika saya bersalah, saya minta maaf (B)

Konklusi : Jika kamu benar, saya minta maaf (B)

d) Silogisma Disjungtif

Premis 1 : p Ú q

Premis 2 : ~ q

Konklusi : p

Jika ada kemungkinan bahwa kedua pernyataan p dan q dapat sekaligus bernilai benar, maka argumen di bawah ini tidak valid.

Premis 1 : p ∨ q

Premis 2 : q

Konklusi : ~ p

Tetapi jika ada kemungkinan kedua pernyataan p dan q tidak sekaligus bernilai benar (disjungsi eksklusif), maka sillogisma disjungtif di atas adalah valid.

Contoh Soal :

1) Premis 1 : Pengalaman ini berbahaya atau membosankan (B)

Premis 2 : Pengalaman ini tidak berbahaya (B)

Konklusi : Pengalaman ini membosankan (B)

2) Premis 1 : Air ini panas atau dingin (B)

Premis 2 : Air ini panas (B)

Konklusi : Air ini tidak dingin (B)

3) Premis 1 : Obyeknya berwarna merah atau sepatu

Premis 2 : Obyek ini berwarna merah

Konklusi : Obyeknya bukan sepatu (tidak valid)

e) Konjungsi

Premis 1 : p

Premis 2 : q

Konklusi : p Ù q

Artinya : p benar, q benar. Maka p Ù q benar.

f) Tambahan (Addition)

Premis 1 : p

Konklusi : p Ú q

Artinya : p benar, maka p Ú q benar (tidak peduli nilai benar atau nilai salah yang

dimiliki q).

g) Dilema Konstruktif :

Premis 1 : (p Þ q) Ù (r Þ s)

Premis 2 : ~ q Ú ~ s

Konklusi : ~ p Ú ~ r

J. Bukti dalam Matematika

1. Pembuktian Tidak Langsung

Pembuktian-pembuktian yang telah kita bicarakan di atas, merupakan pembuktian yang langsung. Suatu argumen adalah valid secara logis jika premis-premisnya bernilai benar dan konklusinya juga bernilai benar. Berdasarkan pemikiran ini, jika premis-premis dalam suatu argumen yang valid membawa ke konklusi yang bernilai salah, maka paling sedikit ada satu premis yang bernilai salah. Cara pembuktian ini disebut pembuktian tidak langsung atau pembuktian dengan kontradiksi atau reductio ad absurdum.

Contoh Soal :

Premis 1 : Semua manusia tidak hidup kekal (Benar)

Premis 2 : Chairil Anwar adalah manusia (Benar)

Buktikan bahwa “Chairil Anwar tidak hidup kekal” (premis 3) dengan melakukan pembuktian tidak langsung.

Bukti :

Kita misalkan bahwa : Chairil Anwar hidup kekal (premis 4) (dan kita anggap bernilai benar).

Maka berarti : Ada manusia hidup kekal (premis 5).

Tetapi premis 5 ini merupakan negasi dari premis 1. Yang sudah kita terima kebenarannya.

Oleh karena itu premis 5 ini pasti bernilai salah.

Karena premis 5 bernilai salah maka premis 4 juga bernilai salah. Sebab itu premis 3 bernilai benar.

Jadi terbukti bahwa “Chairil Anwar tidak hidup kekal”.

Ringkasannya, kita dapat membuktikan bahwa suatu pernyataan bernilai benar, dengan menunjukkan bahwa negasi dari pernyataan itu salah. Ini dilakukan dengan menurunkan konklusi yang salah dari argumen yang terdiri dari negasi pernyataan itu dan pernyataan atau pernyataan-pernyataan lain yang telah diterima kebenarannya.

LATIHAN SOAL

1. Amati pernyataan berikut ini:

p : Hari ini ahmad pergi ke toko buku

q : Hari ini ahmad pergi ke supermarket

Ubah kedua pernyataan diatas dengan logika matematika di bawah ini:

A. p Ù q

B. p Ù ~q

C. ~ p Ù q

D. ~ p Ù ~q

2. Tentukan konvers, invers dan kontraposisi dari pernyataan di bawah ini:

"Jika hari ini hujan maka Wayan mengendarai mobil"

3. Tentukan kesimpulan dari premis berikut:

Premis 1 : Jika Panji rajin belajar maka ia lulus ujian

Premis 2 : Jika Panji lulus ujian maka ia masuk universitas

4. Tentukan negasi dari pernyataan:

a) Bogor hujan lebat dan Jakarta tidak banjir.

b) Hari ini tidak mendung dan Budi membawa payung

5. Tentukan nilai kebenaran pernyataan majemuk dari (~p ∧ r) ∨ (~r ⇒ q)

KUNCI JAWABAN

1. Penyelesaian :

A. p Ù q : Hari ini Ahmad pergi ke toko buku dan supermarket

B. p Ù ~q : Hari ini Ahmad pergi ke toko buku dan tidak ke supermarket

C. ~ p Ù q : Hari ini Ahmad tidak pergi ke toko buku tetapi ke supermarket

D. ~p Ù ~q : Hari ini Ahmad tidak pergi ke toko buku dan tidak ke supermarket

2. Penyelesaian :

Pernyataan di atas adalah implikasi p Þ q sehingga:

p : Hari ini hujan

q : Wayan mengendarai mobil

Konvers dari pernyataan tersebut adalah q Þ p

"Jika Wayan mengendarai mobil maka hari ini hujan"

Invers dari pernyataan di atas adalah ~p Þ ~q

"Jika hari ini tidak hujan maka Wayan tidak mengendarai mobil"

Kontraposisi dari pernyataan tersebut adalah ~q Þ ~p

"Jika Wayan tidak mengendarai mobil maka hari ini tidak hujan"

3. Penyelesaian :

Kita gunakan prinsip silogisme

Premis 1 : p Þ q

Premis 2 : q Þ r

Konklusi : p Þ r

Maka kesimpulannya adalah : "Juka Panji rajin belajar maka ia masuk universitas"

4. Penyelesaian :

Ingkaran (negasi) dari konjungsi.

a) Bogor hujan lebat dan Jakarta tidak banjir.

Ingat:

~(p ∧ q ) º ~p ∨ ~q

Sehingga ingkarannya adalah:

Bogor tidak hujan lebat atau Jakarta banjir.

Hari ini tidak mendung dan Budi membawa paying

Ingat:

~(p ∧ q ) º ~p ∨ ~q

Sehingga ingkarannya adalah:

Hari ini mendung atau Budi tidak membawa paying

5. Penyelesaian :

BAGIAN III

PENUTUP

A. KESIMPULAN

Logika Matematika atau Logika Simbol ialah logika yang menggunakan bahasa Matematika, yaitu dengan menggunakan lambang-lambang atau simbol- simbol. Keuntungan atau kekuatan bahasa simbol adalah: ringkas, univalent/bermakna tunggal, dan universal/dapat dipakai dimana-mana.

Mata pelajaran Logika Matematika mempelajari beberapa hal yang berkaitan dengan logika, seperti logika secara kalimat, logika dalam pemrograman dan logika dalam rangkaian digital. Logika dalam kalimat dinyatakan sebagai proposisi dan pola-pola argumen/pernyataan logis dengan hukum-hukum logika. Logika dalam pemrograman diperlihatkan dengan struktur dasar dari pemrograman dan aliran/kontrol program dengan flow chart. Logika dalam rangkaian digital diperlihatkan dengan logika biner dan gerbang-gerbang logika serta penyederhanaan dalam rangkaian.

Di dalam pembelajaran logika matematika ini membahas tentang pernyataan majemuk beserta negasinya, hukum-hukum logika, kontradiksi, tautologi, ekuivalensi pernyataan-pernyataan majemuk, dan juga penarikan kesimpulan.

B. SARAN

1. Diharapkan siswa dapat memahami mata pelajaran logika matematika dan mengaplikasikannya dalam kehidupan nyata.

2. Penulis dalam menulis makalah ini menyadari masih banyak kekurangan, oleh karena itu pembaca diharapkan memberikan kritik dan saran jika menemukan kesalahan dalam penulisan makalah ini.

DAFTAR PUSTAKA

Anonym. 2013. ”disjungsi nilai kebenaran pernyataan” (online),

http://mafia.mafiaol.com/2013/06/disjungsi-nilai-kebenaran-pernyataan.html, diakses tanggal 25 Maret 2016

Blogspot. 2014. “Makalah Logika Matematika” (online),

(http://irwansahaja.blogspot.co.id/2014/11/makalah-logika-matematika.html), diakses tanggal 25 Maret 2016

Joko, jokom 42. 2012. “logika-matematika” (online),

https://jokom42joko.wordpress.com/2012/01/04/logika-matematika/, diakses tanggal 27 Maret 2016

Matematikastudycenter. ”sma soal pembahasan logika matematika” (online),

http://matematikastudycenter.com/kelas-10-sma/93-10-sma-soal-pembahasan-logika-matematika, diakses tanggal 23 Maret 2016

Rumusmatematikadasar. 2015. ”contoh soal logika matematika dan pembahasannya sma kelas 10” (online),http://www.rumusmatematikadasar.com/2015/01/contoh-soal-logika-matematika-dan-pembahasannya-sma-kelas-10.html, diakses tanggal 25 Maret 2016

Smartblogmathematic. “ingkaran” (online),

https://smartblogmathematic.wordpress.com/ingkaran/, diakses tanggal 27 Maret 2016