Makalah Fungsi Pemetaan

KATA PENGANTAR

Puji syukur kehadirat Allah SWT yang telah  melimpahan rahmat, inayah, taufik, dan hidayah-Nya sehingga kami dapat menyelesaikan makalah tentang Fungsi atau Pemetaan dalam mata kuliah Pembelajaran Matematika SMA.

Penyusunan makalah ini kami susun untuk memenuhi tugas mata kuliah Pembelajaran Matematika SMA. Dalam penyusunan makalah ini kami mendapat bantuan dari berbagai pihak, maka pada kesempatan ini kami mengucapkan terima kasih kepada:

1.    Bapak Drs. Ariyanto, M.Pd.  selaku Dosen mata kuliah pembelajaran Matematika SMA yang telah memberikan pengarahan dalam penyusunan makalah ini.

2.    Teman – teman kelas 4E yang telah memberikan dukungan dalam penyusunan makalah.

Penyusun menyadari bahwa dalam penyusunan makalah ini terdapat kekurangan, karena keterbatasan kemampuan dan pengetahuan yang ada pada penyusun. Oleh karena itu, penyusun sangat mengharapkan  kritik dan saran dari semua pihak yang bersifat membangun demi kesempurnaan makalah ini.

Surakarta,   Oktober 2017

Penyusun

A.    Latar Belakang ................................................................................      1

B.     Rumusan Masalah ...........................................................................      1

C.     Tujuan .............................................................................................      1

BAB II PEMBAHASAN

A.    Pengertian Fungsi.............................................................................      2

B.     Notasi, Daerah Asal, Daerah Kawan, dan Daerah Hasil

Suatu Fungsi .....................................................................................    3

C.     Jenis-Jenis Fungsi..............................................................................    3

D.    Latihan Soal ......................................................................................    6

BAB III PENUTUP

A.    Kesimpulan  ......................................................................................    8

B.     Saran .................................................................................................    8

Daftar Pustaka ..............................................................................................    9

BAB I

PENDAHULUAN

A.    Latar Belakang

Matematika merupakan salah satu disiplin ilmu yang sangat erat dengan suatu bilangan. Matematika juga merupakan bahasa, dimana bahasa pada matematika tidak memiliki makna ambigu (ganda) yaitu selalu pasti. Matematika banyak memegang peran penting dalam pemecahan masalah disetiap bidang kehidupan. Kemampuannya menerjemahkan berbagai fenomena kehidupan dalam bahasa matematika sebagai ilmu dasar yang harus dikuasai oleh setiap orang.

Hubungan antara satu elemen himpunan tepat dengan satu elemen pada himpunan yang lain disebut fungsi. Dalam fungsi ada yang dikenal dengan grafik, grafik fungsi ini menggambarkan hubungan matematik antara dua variabel atau lebih.

B.     Rumusan Masalah

1.    Apakah Pengertian Fungsi atau Pemetaan ?

2.    Apakah Notasi dari Suatu Fungsi?

3.    Apa saja jenis-jenis Fungsi?

4.    Bagaimana bentuk latihan soal Materi Fungsi?

C.    Tujuan

1.    Untuk mengetahui pengertian Fungsi atau Pemetaan.

2.    Untuk mengetahui Notasi dari suatu Fungsi.

3.    Untuk mengetahui jenis- jenis Fungsi.

4.    Mengetahui bentuk latihan soal Materi Fungsi.

BAB II

PEMBAHASAN

A.    Pengertian Fungsi

Fungsi atau pemetaan dari himpunan A ke himpunan B adalah relasi khusus yang memasangkan setiap anggota A dengan tepat satu anggota B.

Ada dua syarat yang harus dipenuh supaya relasi tersebut dapat dikatakan sebagai fungsi yakni:

Pertama, setiap anggota A mempunyai pasangan di B. Jika ada salah satu anggota A tidak memiliki pasangan di B, maka relasi tersebut bukan fungsi.

Kedua, setiap anggota A dipasangkan dengan tepat satu anggota B. Jika anggota A memilik lebih dari satu pasangan maka relasi itu bukan fungsi. Syarat kedua ini tidak berlaku untuk sebaliknya, maksudnya jika syarat pertama dipenuhi anggota B boleh memiliki pasangan lebih dari satu di anggota A.

Contoh:

Pada diagram panah diatas yang merupakan pemetaan adalah diagram (I) dan (III), karena pada diagram (I) dan (III) himpunan A sudah tepat memiliki satu pasangan. Sedangkan untuk diagram (II) dan (IV) bukan pemetaan, karena ada himpunan A yang tidak memiliki pasangan di himpunan B.

B.    Notasi, Daerah Asal, Daerah Kawan, dan Daerah Hasil Suatu Fungsi

Fungsi f dari himpunan A ke himpunan B ditulis :

 f: A→B (dibaca: fungsi f memetakan A ke B)

       Apabila f memetakan suatu x anggota A (x € A) ke suatu y anggota B (y € B) maka y disebut peta dari x oleh f atau y=f(x), sedangkan x disebut prapeta dari f(x). Jika f memetakan setiap x € A ke f(x) € B maka f: A→B ditentukan oleh f:x →f(x) dengan f(x) menyatakan rumus fungsi dari f. Untuk suatu a € A maka f(a) merupakan nilai fungsi f untuk x = a.

Selanjutnya, pada fungsi f : A→B berlaku pula hal-hal sebagai berikut:

a.       Himpunan A disebut daerah asal (domain) dari f, ditulis D

b.      Himpunan B disebut daerah kawan (kodomain) dari f

c.       Himpunan dari semua peta f di B disebut daerah hasil (range) dari fungsi tersebut, ditulis Rf. Tampak bahwa Rf adalah himpunan bagian dari kodomain.

C.    Jenis-Jenis Fungsi

1.      Fungsi Injektif (satu-satu)

Apabila setiap anggota di A dipetakan pada dua anggota yang berbeda di B maka f : A → B disebut fungsi injektif atau satu-satu. Dengan kata lain, suatu fungsi f : A→B disebut fungsi injektif apabila untuk a₁ ≠ a₂, berakibat f(a₁) ≠ f(a₂) atau ekuivalen dengan jika f(a₁) = f(a₂), berakibat a₁ = a₂.

 

Contoh:

a.       Fungsi f : A → B yang didefinisikan oleh f (x) = 2x

b.      Fungsi f : R → R (R € himpunan bilangan real) yang didefinisikan oleh f(x) = x² bukan fungsi satu-satu sebab f (-2) =(-2)² =(2)²= f (2).

2.      Fungsi Surjektif (Onto)

         Misalkan f adalah suatu fungsi yang memetakan A ke B maka daerah hasil f(A) dari f adalah himpunan bagian dari B atau f(A) C B. Jika f(A) = B yang berarti setiap anggota di B pasti merupakan peta dari sekurang-kurangnya satu anggota di A maka dikatakan f adalah fungsi surjektif atau “f memetakan A onto B”. Fungsi surjektif f : A→B ditunjukkan pada gambar berikut,

Contoh:

a.       Misal A = {1,2,3} dan B = {1}. Fungsi f : A→B yang didefinisikan oleh f(x) = 1 adalah fungsi surjektif, sebab daerah hasil dari f sama dengan kodomain dari f.

b.      Fungsi f : R→R yang didefinisikan oleh f(x) = x² bukan fungsi surjektif, sebab himpunan bilangan negatif tidak dimuat oleh hasil fungsi tersebut.

3.      Fungsi Bijektif (Korespondensi satu-satu)

Jika suatu fungsi f : A→B merupakan fungsi injektif sekaligus fungsi surjektif, maka f adalah fungsi yang bijektif atau “A dan B berada dalam korespondensi satu-satu” seperti pada gambar berikut,

Contoh:

a.       Fungsi yang memasangkan bilangan real ke dirinya sendiri atau      f : R→ R yang dirumuskan oleh f(x) = x, jelas merupakan fungsi yang bijektif.

b.      Fungsi f yang memasangkan setiap negara di dunia dengan Ibukota negara-negara di dunia adalah fungsi bijektif karena tidak ada satu kota pun yang menjadi Ibukota dua negara yang berlainan.

4.      Grafik Suatu Fungsi

f(x) = ax+b → garis lurus

f(x) = ax²+bx + c  → parabola

contoh:

Suatu fungsi f didefinisikan dengan f:x → x+4 dengan daerah asal {x l -4 ≤ x ≤2, x R}. Grafik Cartesius fungsi tersebut adalah...

Jawab: f(x) atau y = x+4

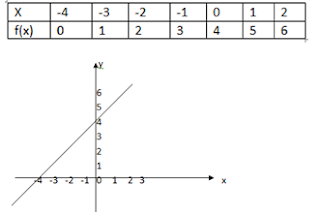
Himpunan titik yang ditebalkan pada gambar tersebut grafik fungsi f : A→B yang ditentukan oleh f : x→f(x).

Selanjutnya, dengan membuat tabel suatu fungsi yang menyatakan daerah asal dan daerah hasil fungsi tersebut, dapat dibuat grafik dengan mudah.

D.    Latihan soal

1.   Dari diagram-diagram panah berikut, manakah yang merupakan fungsi?

Solusi:

a. Diagram panah (a) merupakan fungsi karena setiap anggota A dipasangkan dengan tepat satu anggota B.

b. Diagram panah (b) bukan merupakan fungsi karena ada anggota A, yaitu a, mempunyai dua pasangan anggota B, yaitu 1 dan 2.

c. Diagram panah (c) bukan merupakan fungsi karena ada anggota A, yaitu a, tidak mempunyai pasangan anggota B

2.   Diketahui dua himpunan bilangan A = {4, 5, 6, 7} dan B = {0, 1, 2, 3, 4, 5}. Jika relasi himpunan A ke himpunan B adalah "lebih dari", gambarkan diagram Cartesiusnya.

Solusi:

Diketahui: A = {4, 5, 6, 7} , B = {0, 1, 2, 3, 4, 5}

Relasi himpunan A ke himpunan B adalah "lebih dari".

Jadi, diagramnya adalah sebagai berikut.

3.   Perhatikan diagram panah berikut.

Diagram panah tersebut menunjukkan fungsi himpunan P ke himpunan Q dengan relasi "dua kali dari". Tentukanlah domain, kodomain, dan range fungsinya.

Solusi:

• Domainnya (Df) adalah P = {4, 6, 8, 10}

• Kodomainnya adalah Q = {1, 2, 3, 4, 5}

•Rangenya (Rf) adalah {2, 3, 4, 5}

BAB III

PENUTUP

A.    Kesimpulan

Suatu fungsi f dari himpunan A ke himpunan B adalah suatu relasi yang memasangkan setiap elemen dari A secara tunggal,  dengan elemen pada B. Ditulis f : A → B dibaca “fungsi f  pemetaan A ke dalam / into B”. Apabila f memetakan suatu elemen x ∈ A ke suatu y ∈ B dikatakan bahwa y adalah peta dari x oleh f dan peta ini dinyatakan dengan notasi f(x), dan biasa ditulis dengan f:x → f(x), sedangkan x biasa disebut prapeta dari f(x). Himpunan A dinamakan daerah asal (domain) dari fungsi f , sedangkan himpunan B disebut daerah kawan (kodomain) sedangkan himpunan dari semua peta di B dinamakan daerah hasil (range) dari fungsi f tersebut.

B.    Saran

Konsep “fungsi” terdapat hampir dalam setiap cabang matematika,  sehingga merupakan suatu yang sangat penting artinya dan  banyak sekali kegunaannya. Akan tetapi pengertian dalam matematika agak berbeda dengan pengertian dalam kehidupan sehari-hari. Dalam pengertian sehari hari, “fungsi” adalah guna atau manfaat. Kata fungsi dalam matematika sebagaimana diperkenalkan oleh Leibniz (1646-1716) yang gambarnya terlihat di atas digunakan untuk menyatakan suatu hubungan atau kaitan yang khas antara dua himpunan.

DAFTAR ISI

                                                   

Sunardi,dkk.Pengembangan Matematika Kelas X. Jakarta:Bumi Aksara.

Siswanto.2009.Theory and Application of Mathematics. Solo:Bilingual.

Tuntas Matematika Kelas X.Neutron.

http://www.crayonpedia.org/mw/BAB_2._FUNGSI (online)

http://www.academia.edu/7261122/Materi_Relasi_dan_Fungsi_SMA kelas_X_Perangkat_Pembelajaran  (online)

Jika Sobat Wikimatematika ingin mendapatkan file dokumen ini langsung saja KLIK DISINI

Tweet