Makalah Matriks

KATA PENGANTAR

Assalamualaikum Wr.Wb

     Puji syukur kita panjatkan kepada Allah Subhanahuataala, sholawat serta salam kita kirimkan kepada junjungan kita Nabi Muhammad sallallahualaihiwasallam, karena atas rahmat dan hidayah-Nya peper ini dapat diselesaiakan. Peper ini penulis samapikan kepada Pembina matakuliah Pembelajaran Matematika SMA bapak Ariyanto, sebagai tugas pendalaman pembelajaran matematika. 
     Tidak lupa penulis ucapkan terimakasih kepada bapak maupun ibu dosen matematika yang telah mencurahkan ilmunya kepada penulis, sehingga penulis dapat dengan baik dan lancar dalam menulis paper ini. 
     Selanjutnya kami mohon kepada bapak bapak doseb khususnya dan para pembaca pada umumnya bila ada kesalahan atau kekurangan dalam paper ini, baik dari segi bahasa maupun kontennya, penulis mengharapkan kritik dan saran yang bersifat membangun kepada semua pembaca demi lebih baiknya karya-karya tulis yang akan dating.

Wassalamualaikum Wr.Wb

DAFTAR ISI

KATA PENGANTAR…………………………….ii

DAFTAR ISI ………………………………………iii

BAB I   : PENDAHULUAN

A.    Latar Belakang Masalah ……………….1

B.     Masalah………………………………… 2

C.     Tujuan…………………………………   2

BAB II  : PEMBAHASAN

A.    Pengertian Matriks……………………… 3

B.     Jenis-Jenis Matriks……………………4

C.     Transpose Matriks……………………7

D.    Kesamaan Dua Matriks………………7

E.     Oprasi Penjumlahan dan Pengurangan Matriks…...8

BAB III   : SIMPULAN…………………………..15

DAFTAR PUSTAKA……………………………16

BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Matematika berasal dari bahasa latin Manthanein atau Mathema yang berarti “belajar atau hal yang dipelajari”. Sedangkan matematika di dalam bahasa belanda dikenal dengan sebutan wiskunde yang memiliki arti “ilmu pasti”. Jadi secara umum dapat diartikan bahwa matematika merupakan sebuah ilmu pasti yang berkenaan dengan penalaran.

 Minimnya pemahaman siswa terhadap konsep matematika menimbulkan kesulitan dalam menyelesaikan soal matematika tidak hanya disebabkan oleh siswa itu sendiri, tetapi didukung juga oleh ketidak mampuan guru menciptakan situasi yang dapat membuat siswa tertarik pada pelajaran matematika.

Dalam pembelajaran di Sekolah Menengah Atas (SMA), matriks merupakan materi yang harus dipelajari karena materi ini selalu muncul dalam soal Ujian Nasional (UN), khusus untuk materi matriks ditemukan banyak kendala dalam mempelajarinya.

Impilikasi dirasakan oleh tenaga pengajar (guru) berupa kendala dan hambatan dalam mengajarkan konsep Matriks. apabila guru menerapkan materi yang telah direncanakan, maka sebagian siswa tidak dapat mengikuti dan memahami dengan baik materi tersebut, sehingga pada saat diberikan soal-soal untuk diselesaikan, banyak diantara mereka yang kurang mampu atau mengalami kesulitan dalam menyelesaikan soal-soal tersebut.

Disini penulis akan memberikan materi yang berkaitan  dengan pembahasan Matrik untuk memenuhi tugas Pembelajaran Matematika SMA.

B. Masalah

1.      Apa pengertian Matriks atau pengertian matrik?

2.      Apa  jenis-jenis matrik?

3.      Bagaiman menghitung oprasi hitung penjumlahan dan pengurangan matriks?

4.      Apa itu transpose matrik dan kesamaan matriks?

5.      Bagaiman menyelesaikan soal-soal hitung matrik?

C.  Tujuan masalah

1.      Mengtiatahui pengertian matriks

2.      Mengetahui jenis-jenis matriks

3.      Dapat menghitung oprasi penjumlahan dan pengurangan pada matriks

4.      Mengetahi matriks tanspose dan kesaman matriks

5.      Dapat menyelesaikan soal-soal menhitung matriks.

BAB II

PEMBAHASAN

A.  Pengertian Matriks

Matriks adalah susunan kumpulan bilangan yang di atur dalam baris dan kolom berbentuk persegi panjang. Matrik di cirikan dengan elemen-elemen penyusun yang diapit oleh tanda kurung siku [ ] atau tanda kurung biasa ( ).

Ukuran sebuah matrik dinyatakan dalam satuan ordo, yaitu banyaknya baris dan kolom dalam matriks tersebut. Ordo merupakan karakteristik suatu matriks yang menjadi patokan dalam oprasi-oprasi antar matriks. Matriks pada umumnya di simbolkan seperti berikut ini :

Keterangan :

A             = nama matrik

m             = banyak baris

n              = banyak kolom

m x n       = ordo matriks

Amxn      =artinya elemen matrik baris ke-m kolom ke-n.

Contoh 1

Tentukan baris dan kolom ?

Jawaban :

2 adalah elemen baris ke-1 kolom ke-1

4 adalah elemen baris ke-2 kolom ke-2

7 adalah elemen baris ke-3 kolom ke-2

B.  Jenis – Jenis Matriks

a.    Matriks persegi

     Suatu matriks yang memiliki banyaknya baris sama dengan banyaknya kolom disebut matriks persegi.
 Contoh 2.

b.    Matriks Baris

     Matriks yang hanya mempunyai satu baris saja disebut matriks baris. Ordo matriks baris ditulis (1xn) dengan n > 1, dan bilangan asli.
 Contoh 3
 

c.    Matriks Kolom

     Matriks yang hanya mempunyai satu kolom saja disebut matriks kolom. Ordo matriks kolo ditulis (mx1) dengan m ≥ 2, dan bilangan Asli.
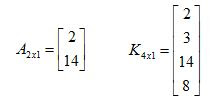
Contoh 4
 

   
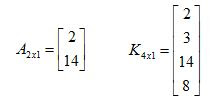
d. Matriks Diagonal 
     Matriks diagonal adalah matriks persegi yang semua elemen atau unsur di luar diagonal utamanya adalah nol.
Contoh 5

e. Matriks Identitas

     Suatu matriks dikatakn identitas, apabila diagonal yang elemen-elemen atau unsure-unsur diagonal utama bernilai 1 (satu).
Contoh 6

f. Matriks Nol

     Dikatakan sebagai matriks nol, apabila semua elemen atau unsurnya adalah nol.

Contoh 7

g. Matriks Simetris/Setangkap

     Matriks Simetris adalah matriks persegi yang unsur padabaris ke-n dan kolom ke-m sama dengan unsure pada baris ke-m kolom ke-n.

 Contoh 8

h. Matriks Segitiga

     Matriks segitiga adalah matriks persegi yang mempunyai elemen-elemen di atas diagonal utamanya bernilai nol atai elemen-elemen di bawah diagonal utamanya bernilai nol.
Contoh 9

C.  Transpose Matriks

     Transpose dari suatu matriks Amxn dapat dibentuk dengan cara menukarkan baris matriks A menjadi kolom matriks baru dan kolom matriks A menjadi matriks baru. Mtriks baru dinyatakan dengan lambang
Contoh 10

D.  Kesamaan Dua Matriks

      Dua buah matriks A dan B dikatakan sama (ditulis A=B), jika dan hanya jika kedua matriks itu mempunyai ordo yang sama dan elemen-elemen yang seletaknya sama. Karena menggunakan “jika dan hanya jika” maka pengertian ini berlaku menurut dua arah, yaitu:
a.  Jika A=B maka haruslah ordo kedua matriks itu sama, dan elemen-elemen yang seletak sama.
b. Jika dua buah matriks mempunyai ordo yang sma, elemen-elemen yang seletak juga sama maka A=B.
Contoh 11a

Contoh 11b

E.  Operasi Aljabar pada Matriks

a. Penjumlahan Matriks 
     Jika A dan B dua buah matriks berordo sama maka jumlah matriks A dan B ditulis A+B adalah sebuah matriks baru C yang diperoleh dengan menjumlahkan elemen-elemen matriks A dengan elemen-elemen B yang seletak.
Contoh 12

Pada penjumlahan belaku sifat- sifat :

1.      Komutatif, A+B = B+A

2.      Asosiatif, ( A+B)+C = A+(B+C)

3.      Sifat lawan, A+(-A) = 0

4.      Identitas penjumlahan, A+0 = A

b. Pengurangan Matriks 
     Pengurangan matriks A dengan matriks B adalah suatu matriks yang elemen-elemenya diperoleh dengan cara mengurangkan elemen matriks A dengan elemen matriks B yang besesuaian (seetak), atau dapat pula diartikan sebagai menjumlahkan matriks A dengan lawan negative dari B, dituliskan: A-B = A+(-B). 
     Seperti halnya pada penjumlahan dua buah matriks, pengurangan dua buah matriks pun terdefinisi apabila ordo kedua matriks tersebut sama.
c. Soal-Soal dan penyelesaian Matriks.


 

 
  

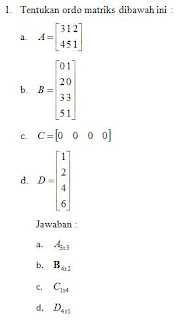
BAB III

PENUTUP

A.  Kesimpulan

       Matriks adalah susunan kumpulan bilangan yang di atur dalam baris dan kolom berbentuk persegi panjang. Matrik di cirikan dengan elemen-elemen penyusun yang diapit oleh tanda kurung siku [ ] atau tanda kurung biasa ( ). Ukuran sebuah matrik dinyatakan dalam satuan ordo, yaitu banyaknya baris dan kolom dalam matriks tersebut.

        Transpose dari suatu matriks Amxn dapat dibentuk dengan cara menukarkan baris matriks A menjadi kolom matriks baru dan kolom matriks A menjadi matriks baru.

         Dua buah matriks A dan B dikatakan sama (ditulis A=B), jika dan hanya jika kedua mempunyai ordo yang sama dan elemen-elemen yang seletaknya sama.

          Penjumlahan Matriks Jika A dan B dua buah matriks berordo sama maka jumlah matriks A dan B ditulis A+B adalah sebuah matriks baru C yang diperoleh dengan menjumlahkan elemen-elemen matriks A dengan elemen-elemen B yang seletak.

        Pengurangan Matriks Pengurangan matriks A dengan matriks B adalah suatu matriks yang elemen-elemenya diperoleh dengan cara mengurangkan elemen matriks A dengan elemen matriks B yang besesuaian (seetak), atau dapat pula diartikan sebagai menjumlahkan matriks A dengan lawan negative dari B, dituliskan: A-B = A+(-B).

          Pada penjumlahan dan pengurangan belaku sifat- sifat :

1.      Komutatif, A+B = B+A

2.      Asosiatif, ( A+B)+C = A+(B+C)

3.      Sifat lawan, A+(-A) = 0

4.      Identitas penjumlahan, A+0 = A

DAFTAR PUSTAKA

Mauludin, Ujang. 2005.Matematika Program Ilmu Alam untuk SMA atau MA XII.Bandung: PT Sarana Panca Karya Nusa

 Opan.definisi dan jenis matriks (http://uhyan.com/definisi-dan-jenis-matriks.php) .Diakses tanggal 01 April 2016

Jika sobat ingin mendapatkan file makalah ini. KLIK DISINI GRATIS.....

Tweet