loading...
loading...
» » MAKALAH ATURAN PERKALIAN DAN PERMUTASI
Edit

MAKALAH ATURAN PERKALIAN DAN PERMUTASI

KATA PENGANTAR


            Puji syukur kehadirat Tuhan Yang Maha Esa karena atas limpahan rahmat dan karunia-Nya, kepada saya dalam menyusun tugas makalah ini yang berjudul Makalah Pembelajaran Matematika SMA Pokok Bahasan Aturan Perkalian dan Permutasi ini dengan sebaik-baiknya, walaupun masih jauh dari kata sempurna. Dalam waktu yang begitu padat saya mencoba untuk mengambil celah-celah agar saya dapat berdiskusi dalam menyelesaikan tugas ini. Ini bukanlah tugas pertama untuk membuat makalah tapi saya tetap bersemangat dalam mengerjakannya.
            Saya juga mengucapkan terima kasih kepada dosen pengampu yang telah membimbing saya dalam melakukan penyusunan tugas ini. Tak lupa juga saya sampaikan kepada teman-teman mahasiswa yang telah memberikan referensi dan masukkan bagi saya dalam melakukan pengembangan akan tugas pembelajaran matematika SMA ini.
            Saya sadar bahwa tugas yang saya susun mungkin masih banyak terdapat kekurangan sehingga masih banyak diperlukan perbaikan-perbaikan yang berkesinambungan dalam upaya mendapatkan hasil yang jauh lebih baik. Oleh karena itu, saya mengharapkan kritik dan saran dari pembaca yang sifatnya membangun demi perbaikan makalah ini dan berikutnya.
           
Surakarta, 03 April 2016

Penulis

DAFTAR ISI



KATA PENGANTAR.. ..............................................................................................iiii
DAFTAR ISI. ...........................................................................................................iiiiii
BAB I. ......................................................................................................................11
PENDAHULUAN.. ..................................................................................................11
A.   LATAR BELAKANG.. 1......................................................................................1
B.    RUMUSAN MASALAH.. 1................................................................................1
C.    TUJUAN.. 1.........................................................................................................1
BAB II. 2....................................................................................................................2
PEMBAHASAN.. 2....................................................................................................2
A.   Aturan Perkalian. 2.............................................................................................2
B.    Permutasi 3........................................................................................................3
LATIHAN SOAL.. 9...................................................................................................9
BAB III. 10...................................................................................................................10
PENUTUP. 10..............................................................................................................10
A.   Kesimpulan. 10......................................................................................................10
B.    Saran. 10...............................................................................................................10
DAFTAR PUSTAKA.. 11.............................................................................................11
KUNCI JAWABAN ..............................................................................................1212

BAB I

PENDAHULUAN

A.    LATAR BELAKANG

Dalam materi ini penulis akan membahas teori permutasi. Yang mungkin sudah anda pernah dapat dan pelajari pada waktu SMA kelas XI namun demikian, materi akan diberikan dalam makalah ini bukan hanya sekedar mengulang tetapi diharapkan pula memberikan wawasan yang luas mengenai pendefinisikan permutasi. Untuk dalam mendukung proses lancarnya terhadap penguasaan materi dalam makalah ini juga dipelajari teknik aturan perkalian dan konsep faktorisasi yang membantu dalam memahami permutasi.
Permutasi sering kita temukan dalam kehidupan kita sehari-hari yang membantu kita menyelesaikan suatu masalah, yang tidak kita sadari dengan sendirinya. Oleh karena itu disini saya memberikan pemahaman yan mendalam sehingga kita bisa mengerti dan munggunakan permutasi.

B.     RUMUSAN MASALAH

1.      Apa yang dimaksud dengan aturan perkalian dan perrmutasi ?
2.      Bagaimana penggunaan caran dan konsep dari aturan perkalian dan permutasi ?

C.    TUJUAN

1.    Untuk memahami aturan perkalian dan permutasi.
2.    Untuk memahami penggunaan cara dan konsep dari aturan perkalian dan permutasi. 

BAB II

PEMBAHASAN

A.    Aturan Perkalian

Misalkan pilihan pertama yang ada dianggap sebagai suatu tempat. Jika terdapat n tempat dengan ketentuan :
1.    Banyak cara untuk mengisi tempat pertama adalah c1 ;
2.    Banyak cara untuk mengisi tempat kedua setelah tempat pertama dipenuhi c2 ;
3.    Banyak cara untuk mengisi tempat ketiga setelah tempat pertama dam kedua dipenuhi c3 ;
Dan seterusnya hingga banyak cara untuk mengisi tempat ke-n setelah tempat pertama, kedua, ketiga, ..., ke-( n-1 ) dipenuhi adalah cn.
Banyak cara untuk mengisi n buah tempat secara keseluruhan dapat dirumuskan dengan:
        c1 x c2 x c3 x  ... x cn
Aturan seperti ini disebut aturan perkalian atau aturan pengisian tempat yang tersedia (filling slot):
Contoh :
Disediakan angka-angka 2, 3, 4, 5, dan 6. Tentukan :
a.    Banyak angka ratusan yang dapat dibentuk.
b.    Banyak angka ratusan ganjil yang dapat dibentuk.
c.    Banyak angka ratusan yang lebih besar dari 500 yang dapat dibentuk.
Pembahasan :
a.    Angka ratusan terdiri atas 3 angka

Ratusan            Puluhan             Satuan

5 cara              5 cara                5 cara

Jadi, banyak angka ratusan yang dapat dibentuk adalah 5 × 5 × 5 = 125 angka.

b.    Angka ratusan ganjil yang mungkin terbentuk dari angka-angka itu satuannya adalah 3 dan 5.
Ratusan            Puluhan             Satuan

5 cara              5 cara                2 cara
Jadi, banyak angka ratusan ganjil yang dapat dibentuk adalah 5 × 5 × 2 = 50 angka.
c.    Angka yang lebih besar dari 500 mempunyai angka ratusan 5 dan 6.
Ratusan            Puluhan             Satuan

2 cara              5 cara                2 cara
Jadi, banyak angka ratusan yang lebih besar dari 300 yang dapat dibentuk adalah 2 × 5 × 5 = 50 angka.

B.    Permutasi

Permuatasi adalah susunan suatu objek-objek dari suatu grup dengan memperhatikan urutan. Sebelum kita mempelajari permutasi lebih baiknya kita mulai dengan konsep faktorial.
1.    Faktorial dari Bilangan Asli
Perhatikan perkalian berikut.
3 × 2 × 1 = 3!
4 × 3 × 2 × 1 = 4!
5 × 4 × 3 × 2 × 1 = 5!
Dan seterusnya. Tanda “!” adalah notasi faktorial. Jika n bilangan asli, n faktorial (ditulis n!). Faktorial dari suatu bilangan asli didefinisikan sebagai berikut. 
n! = n x (n-1) x (n-2) x (nx3) x ... x 2 x 2 x 1

Dari definisi di atas, dapat diperoleh
                    n! = n (n-1)
Nilai 1! = 1. Oleh karena itu, untuk n = 1, diperoleh
1! = 1(1-1)!
1  = 0!
                     0! =1
2.    Permutasi dari Unsur-unsur yang Berbeda

Misalkan dari tiga buah angka 1, 2, dan 3 akan disusun suatu bilangan yang terdiri atas tiga angka dengan bilangan-bilangan itu tidak mempunyai angka yang sama. Susunan yang dapat dibentuk adalah :
123             132             213             231             312             321
Banyak cara untuk membuat susunan seperti itu adalah 3 × 2 × 1 = 6 cara.
Susunan yang diperoleh seperti di atas disebut permutasi 3 unsur yang diambil dari 3 unsur yang tersedia.
Berdasarkan deskripsi di atas, permutasi dapat didefinisikan sebagai berikut.
Definisi : 
Permutasi r unsur yang diambil dari n unsur yang tersedia (tiap unsur itu berbeda) adalah susunan dari r unsur itu dalam suatu urutan ( r ≤ n ).
Banyak permutasi r unsur yang diambil dari n unsur yang tersedia dilambangkan dengan notasi :

Jika r = n maka banyak permutasi n unsur yang diambil dari n unsur yang tersedia (biasa disingkat : permutasi n unsur) dilambangkan dengan notasi :

                 Contoh :
Berapa banyak permutasi dari 4 huruf A, B, C, dan D?
Pembahasan :
Sebuah contoh permutasi atau susunan 4 huruf dalam suatu urutan adalah
 huruf pertama         huruf kedua         huruf ketiga         huruf keempat
B                            D                         A                          C

·      Huruf pertama dalam susunan itu dapat dipilih dengan 4 cara, yaitu huruf A, B, C, atau D.
·      Huruf kedua dapat dipilih dengan 3 cara. Misalnya, jika huruf pertama dipilih B maka huruf kedua yang dapat dipilih adalah D, A, atau C.
·     Huruf ketiga dapat dipilih dengan 2 cara. Misalnya, jika huruf pertama dipilih B dan huruf kedua dipilih D, maka huruf ketiga yang dapat dipilih adalah  A, atau C.
·     Huruf keempat dapat dipilih dengan 1 cara. Misalnya, jika huruf pertama dipilih B, huruf kedua dipilih D, dan huruf ketiga dipilih  A, maka huruf keempat tinggal 1 pilihan yaitu huruf C.
Dengan menggunakan aturan perkalian, banyak susunan yang mungkin itu seluruhnya adalah :


Berdasarkan contoh diatas, terlihat bahwa permutasi 4 unsur adalah



Secara umum dapat disimpulkan bahwa :
Banyaknya permutasi n unsur ditentukan dengan aturan :



Contoh :
Berapakah banyak permutasi 2 huruf yang diambil dari huruf-huruf A, B, C, D, dan E ?
Pembahasan :
Sebuah contoh permutasi atau susunan 2 huruf yang diambil dari huruf-huruf A, B, C, D, dan E adalah :
huruf pertama              huruf kedua
D                                 E
·     Huruf pertama dalam susunan itu dapat dipilih dengan 5 cara, yaitu huruf A, atau B, atau C, atau D, atau E.
·      Huruf kedua dapat dipilih dengan $ cara. Misalnya jika huruf pertama dipilih D, maka huruf kedua yang dapat dipilih adalah huruf A, B, C, atau E.
Dengan menggunakan aturan perkalian, banyak susunan yang mungkin itu seluruhnya adalah :


Berdasarkan deskripsi diatas, terlihat bahwa banyak permutasi 2 unsur yang diambil dari 5 unsur yang tersedia adalah :



Secara umum dapat disimpulkan bahwa :
Banyak permutasi r unsur yang diambil dari n unsur yang tersedia ditentukan dengan aturan :



Contoh :
Hitung tiap permutasi berikut :



3.    Permutasi Memuat Beberapa Unsur yang Sama
                 Permutasi n unsur, dengan k unsur sama dan n unsur itu ( n ≥ k ) adalah

Aturan ini dapat diperluas untuk permutasi n unsur, dengan k1 unsur sama, k2 unsur sama, ... , dan kn unsur sama dari n unsur ( k1 + k2 + ... + k1 ≤n ), yaitu



Contoh :
Tentukan banyak susunan huruf yang dapat dibentuk dari unsur huruf-huruf pembentuk TIGA SERANGKAI.
Pembahasan :
Perhatikan kata TIGA SERANGKAI.
Unsur yang tersedia n = 13.
Unsur yang sama adalah
a.       k1 = 2, yaitu huruf I ada 2.
b.      k2 = 2, yaitu huruf G ada 2.
c.       k3 = 3, yaitu huruf A ada 3.
                Jadi, banyak susunan yang dimaksud adalah


4.    Permutasi Siklis
Permutasi siklis adalah permutasi yang dibuat dengan menyusun unsur secara melingkar. Misalkan terdapat n unsur yang berbeda disusun melingkar. Banyak susunan dapat ditentukan dengan permutasi siklis dengan aturan





Contoh :
Misalkan ada 4 orang A (ani), B (Boy), C (Carli), dan D (Doni) menempati empat buah kursi yang mengelilingi sebuah meja bundar. Berapa banyak susunan yang dapat terjadi ?
Pembahasan :
Banyak unsur n = 4  , maka banyak permutasi siklis dari 4 unsur itu seluruhnya ada

Psiklis =  (4 – 1)! = 3! = 3 x 2 x 1 = 6 macam 
Jadi, banyaknya susunan yang dapat terjadi ada 6 macam.



LATIHAN SOAL

1.    Banyak bilangan yang terdiri atas 4 angka yang dapat disusun dari angka-angka 2, 4, 5, dan 6 dengan syarat bilangan yang disusun genap adalah ....
2.    Di dalam sebuah kelas, akan dibentuk kepengurusan yang terdiri atas ketua, sekretaris, dan bendahara kelas. Berapa banyak cara 5 calon yang akan memperebutkan ketiga posisi tersebut adalah ....
3.    Sebanyak 8 orang mengadakan pertemuan. Mereka duduk menghadap sebuah meja bundar. Berapa banyak cara mereka menempati kursi yang disusun melingkar adalah ....
4.    Berapa banyak susunan huruf yang dapat disusun dari huruf-huruf berikut ini :
a.       J, A, K, A, R, T, dan A.
b.      T, R, I, G, O, N, O, M, E, T, R, dan I.



BAB III

PENUTUP

A.    Kesimpulan

Permuatasi adalah susunan suatu objek-objek dari suatu grup dengan memperhatikan urutan. Dalam mempelajari permutasi        diperlukan pemahaman aturan perkalian dan konsep faktorial.
Dari materi aturan perkalian kita bisa dapat menentukan cara perkalian dari suatu data. Permuatsi dibagi dari memuat beberapa unsur uang yang beda, memuat beberapa unsur uang yang sama, dan permutasi siklis sehingga kita tidak lagi kesusahan dalam membedakan dan menggunakannya.

B.     Saran

Demikian makalah yang dapat saya buat, sebagai manusia biasa saya menyadari dalam pembuatan makalah ini masih terdapat banyak kesalahan dan kekurangannya. Untuk itu saya harapkan adanya kritikan dan saran yang bersifat membangun sangat saya harapkan, demi kesempurnaan makalah ini dan berikut-berikutnya. Semoga makalah ini bermanfaat bagi kita semua.



DAFTAR PUSTAKA

Tim Penulis. 2010. Matematika untuk Kelas XI SMA dan MA. Solo: Tiga Serangkai Pustaka Mandiri.
Wirodikromo, Sartono. 2007. Matematika untuk SMA Kelas XI. Jakarta: Erlangga.


KUNCI JAWABAN

Jika Sobat WikiMatematika ingin mendapatkan file makalah secara gratis langsung saja Klik DISINI



































































































































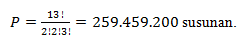
0 Response to "MAKALAH ATURAN PERKALIAN DAN PERMUTASI"

Post a Comment

Subscribe to: Post Comments (Atom)